zur Tabelle der Noten und Frequenzen

Dieser Abschnitt wird in einem eigenen Fenster angezeigt, damit man dieses für mehrfaches Nachsehen bereithalten kann.

Obwohl in den Musikinstrumenten sehr oft die Tonhöhe durch die Länge eines schwingenden Gebildes - Luftsäule, Saite, Stab, auch Membran (dann in zwei Richtungen) - bestimmt wird, denkt man in der Musik nicht so sehr an die Wellenlänge, sondern an die Tonhöhe, die durch die Anzahl der Schwingungen pro Sekunde, genannt die "Frequenz", bezeichnet wird. Die Frequenz hat die Einheit "Hertz" (Hz). Die Wellenlänge und die Frequenz eines Tons hängen mit einer einfachen mathematischen Beziehung zusammen: multipliziert man beide Größen miteinander, ergibt sich stets die Schallgeschwindigkeit. Bis in die Neuzeit - bis zur Zeit Johann Sebastian Bachs - stand aber nicht so sehr die absolute Tonhöhe eines einzelnen Tons im Vordergrund, sondern vielmehr das Verhältnis zweier oder mehrerer Töne zueinander, also die Intervalle. Der Grund hierfür ist, dass man die Frequenz nicht messen konnte. Erst 1939 wurde in einer internationalen Empfehlung die Frequenz des Kammertons auf 440 Hz festgelegt.

Der Kammerton war davor auf niedrigeren Frequenzen, zu Bachs Zeiten etwa bei 435 Hz, und wurde langsam in die Höhe geschraubt, weil die Violinen dann "strahlender" - d. h. obertonreicher - klingen. Inzwischen ist es durchaus üblich, den Kammerton auf 442 Hz, ja sogar 443 Hz anzusetzen. Bei Blasorchestern ist diese Mode auch zu finden, nur fehlt noch eine vernünftige Begründung dafür. Gerade die Klarinette läßt sich nicht beliebig umstimmen.

Schon im Altertum - also vor mehr als 2000 Jahren - wußte man, dass es sich, was die Intervalle betrifft, um zahlenmäßig genau definierte Verhältnisse von Frequenzen handelt. Die Oktave und die Quinte tun sich dabei besonders hervor: Die Oktave hat genau die doppelte Frequenz, und die Frequenzen des Quintintervalls verhalten sich genau wie 3:2, als Dezimalzahl 1,5. Auch die Terzen und die Sexten haben Frequenzverhältnisse mit kleinen ganzen Zahlen. Diese Intervalle, die als wohltönend empfunden werden, nennt man "rein".

Setzt man zwei Intervalle aneinander, um ein größeres Intervall zu bekommen, muss man die beiden Frequenzverhältnisse miteinander multiplizieren, um das Frequenzverhältnis der beiden äußeren Töne zu bekommen, also bei zwei Quinten ergibt das 2,25.

Mit der Bedingung, dass das Quintintervall genau das Verhältnis 3:2 hat, kommt man aber beim Aufbau einer Tonleiter in einen Widerspruch, mit dem man viele Jahrhunderte lang nicht zurecht kam. Bei den über eine Klaviatur bedienten Instrumenten - Orgel, Cembalo, Spinett, Klavier  mit ihren fest zu stimmenden Tönen konnte man aber nicht mehr umhin, nach einer Lösung zu suchen. Stimmt man ein Klavier in "reiner" Stimmung, was nach Gehör geht, dann erhält man Folgendes: Geht man von Quinte zu Quinte aufwärts, also

C-G-D-A-E-H-Fis-Cis-Gis-Dis-Ais-Eis(F)-C

dann hat man nach 12 Quinten wieder ein C erreicht und dabei alle bei uns gebräuchlichen Töne der Tonleiter erfasst. Die obige Folge nennt man übrigens den "Quintenzirkel aufwärts". Der "Quintenzirkel abwärts" ist von rechts nach links zu lesen:

C-G-D-A-Fes(E)-Ces(H)-Ges-Des-As-Es-B-F-C

Auf einer Klaviatur können wir abzählen, dass zwischen dem unteren und dem oberen C  7 Oktaven liegen. 7 Oktaven bedeuten aber das Frequenzverhältnis von genau 128! Gehen wir dagegen den Quintenzirkel durch, haben wir 1,5 elfmal mit 1,5 zu multiplizieren und erhalten, dass das das C am oberen Ende des Quintenzirkels die 129,746337890625-fache Frequenz wie das C am Anfang des Zirkels hat. Das ist immerhin 23 % eines Halbtons höher, also heftig. Man kommt also um einen kleinen Betrug nicht herum. Teilen wir die Unstimmigkeit gleichmäßig auf, dann erhält eine "Quinte", deren Frequenzverhältnis 12-mal multipliziert genau 128 ergibt, das Frequenzverhältnis 1,49830708... (fünf Dezimalstellen reichen). Von den 23 % Differenz über den ganzen Quintenzirkel hinweg erhält jede Quinte ein Zwölftel zugeschrieben, also nur knappe 2 % eines Halbtons.

Eine Tonskala, bei der alle Intervalle den gleichen Tonabstand haben, nennt man "gleichschwebend", weil bei jeder herausgegriffenen Quinte die Abweichung vom "reinen" Quintintervall die gleiche Schwebung ergibt. Bei Klavieren verwendet man aber gern eine Modifikation der Stimmung, die von Bach mit seinem Werk "Das wohltemperierte Klavier" demonstriert wurde. Die "wohltemperierte Stimmung" gibt Tonarten auf dem Klavier einen eigenen Charakter. Bläser (und Streicher) haben aber kein fest abgestimmtes Instrument, sondern müssen nicht nur momentan den Ton greifen und erzeugen, sondern ihn auch immer noch sofort einstimmen! Dabei haben sie von Ton zu Ton mit viel größeren Abweichungen der Tonhöhen von den geforderten Werten zu kämpfen, nämlich dem Fünf- bis Zehnfachen dessen, was den Unterschied zwischen "gleichschwebend" und "wohltemperiert" ausmacht.

Die folgende Tabelle soll zum Nachschlagen sein, damit man nicht immer von Anfang an rechnen muss.

Zurück zum Anfang

Tabelle der Notennamen und der zugehörigen Frequenzen

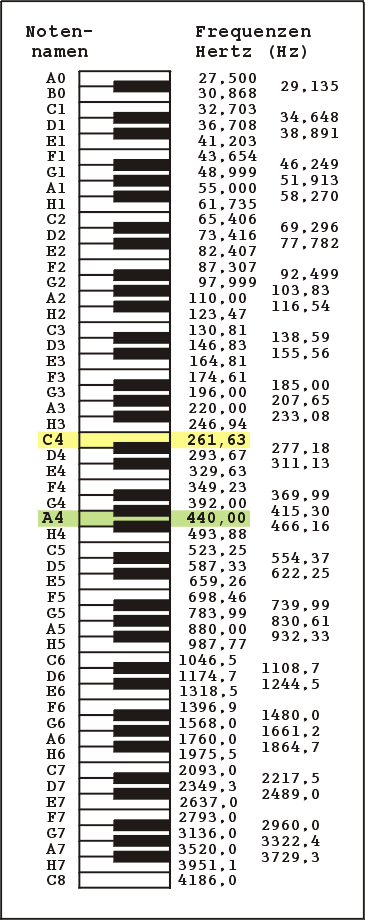Die Tabelle zeigt anhand der Klaviatur die Notennamen und die Frequenzen der Töne, wobei der Kammerton als A4 mit 440 Hz der Norm von 1939 entspricht. Die Frequenzen gelten für die "gleichschwebende Stimmung". Im Standard MIDI (Musical Instruments Digital Interface) werden die Noten durch Zahlen repräsentiert, wobei die MIDI Manufacturers Association nur festgelegt hat, dass die "60" ein "mittleres C" bezeichnet. Die klingenden Töne können also um ein oder sogar mehrere Oktaven variieren. Hier im Bild ist C4 das C, welches den Übergang zwischen den Noten im Violinschlüssel und dem Bassschlüssel bildet. Im Bild der Klaviatur ist dies gelb markiert.

Der Kammerton ist nur mit der Frequenz 440 Hz eindeutig zu bezeichnen, mit der Bezeichnung "A4" ist er leider nicht eindeutig bezeichnet. Ich bin selber schon darauf hereingefallen, dass in meinem Programm zur Musikbearbeitung die Notenbezeichnung um 1 niedriger ist, also für den Kammerton "A3" ist.

Zurück zum Anfang